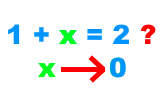
The need for Math is real when diving deep into AI which I found myself scrambling. Thus I made it my mission to brush up on my math.

Branches of Mathematics

Traditional Branches

I do recall the following traditional branches of Math being taught in school but could not say I still know them all:

  • Arithmetic - study of numbers using various operations on them such as addition, subtraction, multiplication, and division
  • Algebra - study of variables, expressions and equations such as linear equations and quadratic equations
  • Geometry - study of shapes such as points, lines, angles, surfaces, and solids
  • Trigonometry - study of triangles specifically side lengths and angles
  • Calculus - study of continuous change or rate of change

And those are just touching the fundamentals as there are also advanced topics within those branches. There is a whole swat of other fields in Math that I do not know. It’s actually so hard to categorize them, classify them, divide them into parts so that it would be easy to navigate between them. I am basically thrown into the ocean or into the math trench on my own, and it’s up to me to navigate them.

Advanced Branches

There are other branches that maybe worth looking into beyond Calculus to further widen your knowledge in Math, explore the math trench as I would say. Here are some of them:

  • Discrete Math - antithesis of Calculus; a broad field involving anything that can be separated into discrete objects, with topics like Formal Logic, Counting Problems, and Graph Theory
  • Real Analysis - heart of Calculus; an important field that provides justification for all of Calculus; studies the behavior of real numbers, sequences and series of real numbers, and real functions
  • Complex Analysis - analysis that takes real functions and extends them to the complex plane; investigates functions of complex numbers
  • Modern/Abstract Algebra - an advanced field in Algebra; the study of algebraic structures such as groups, rings, fields, modules, vector spaces, lattices, and algebras
  • Linear Algebra - study involving linear equations; of lines and planes, vector spaces and mappings that are required for linear transforms
  • Differential Geometry - studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds using differential calculus, integral calculus, linear algebra and multilinear algebra
  • Probability and Statistics - Probability deals with predicting the likelihood of future events, while Statistics involves the analysis of the frequency of past events
  • Numerical Methods - a mathematical tool designed to solve numerical problems in Numerical Analysis, which is the study of algorithms that use numerical approximation for the problems of mathematical analysis
  • Information Theory and Signal Processing - Information Theory is the scientific study of the quantification, storage, and communication of digital information while Signal Processing is analyzing, modifying, and synthesizing signals such as sound, images, and scientific measurements

Branches for AI

And there are these branches of Math that you will need when diving deep into AI. Besides Linear Algebra, the following are some of them:

  • Analytic Geometry - also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system
  • Matric Decompositions - in linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices
  • Vector Calculus - or vector analysis, is concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space $ R^3 $
  • Probability and Distributions - in Probability and Statistics, a probability distribution is a statistical function that describes all the possible values and likelihoods that a random variable can take within a given range
  • Continuous Optimization - as opposed to Discrete Optimization, the variables used in the objective function are required to be continuous variables—that is, to be chosen from a set of real values between which there are no gaps

Specific Concepts for AI

To be more specific, the following are some of the concepts you will need:

  • In Algebra, they are the Exponents, Radicals, Factorials, Summations, Scientific Notations
  • In Linear Algebra, they are the Scalars, Vectors, Matrices, Tensors, Eigenvectors & Eigenvalues, Singular Value Decomposition, Principal Component Analysis (PCA)
  • In Calculus, they are the Derivatives, Vector/Matrix Calculus, Gradient Algorithms
  • In Probability and Statistics, they are the Basic Statistics, Basic rules in probability, Random variables, Bayes’ Theorem, Maximum Likelihood Estimation (MLE), Common Distributions
  • In Information Theory, they are the Entropy, Cross-Entropy, Kullback Leibler Divergence, Viterbi Algorithm, Encoder-Decoder

To learn more about these concepts, check this article All the Math You Need to Know in Artificial Intelligence.

As you can see now, it’s really daunting how much math you need to know when getting into AI. I don’t expect to know them all at once but at least I know for now what they are which I can get into more depth as needed.

Solving Equations

For now it would be wise to know how to solve equations as I find this will help in understanding the formulas, computations, or calculations that abound in AI.

Techniques

To solve equations, you need to know some basic techniques and these techniques are:

  • Add or Subtract the same value from both sides (the balancing method)
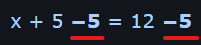
  • Clear out any fractions by Multiplying every term by the bottom parts, and in case of multiple fractions multiplying by their LCD
  • If there are decimals, multiply both sides of the equation by the lowest power of 10 to convert them into whole numbers
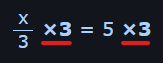
  • Divide every term by the same nonzero value
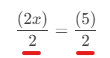
  • Combine Like Terms
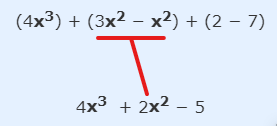
  • Factoring and using Distributive Property
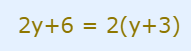
  • Expanding (the opposite of factoring) may also help
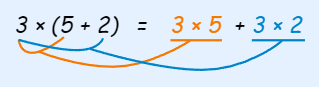
  • Recognizing a pattern, such as the difference of squares
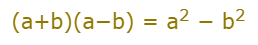
  • Sometimes we can apply a function to both sides (e.g. square both sides)

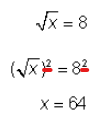
Rules, Formulas, Properties

The rules, formulas, and properties in the different fields of Mathematics are tools for solving equations. You need to know them as well. The following infographics lists some of them.

Algebra

In Algebra you have: associative, commutative, and distributive properties; arithmetic operations rules; properties of exponents, radicals, inequalities, absolute values, complex numbers, logarithms, and polynomials; common factoring techniques; quadratic equation formula.

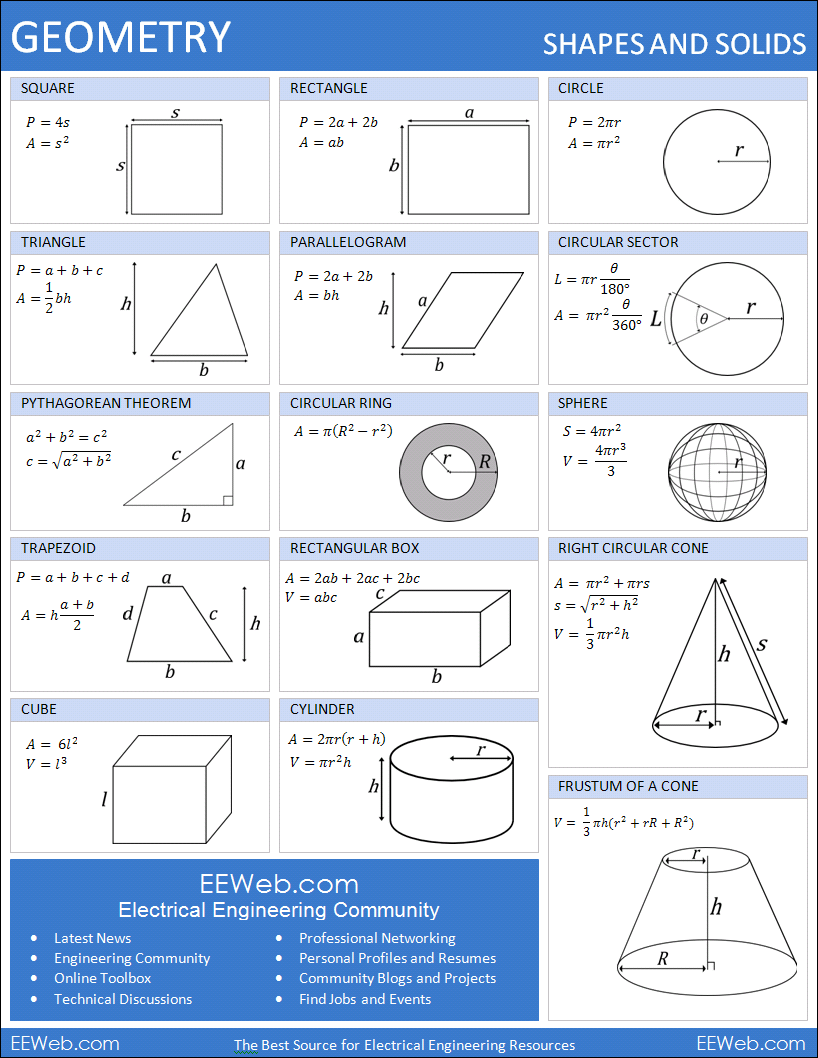
Geometry

In Geometry you have: circumference and area formulas for square, rectangle, circle, triangle, parallelogram, and trapezoid; area of a circular ring as well as the area and segment length of a circular sector; area and volume of rectangular box, cube, and cylinder; area, side length, and volume of a right circular cone, as well as the volume of a frustum of a cone; pythagorean theorem.

Trigonometry

In Trigonometry you have: right triangle definitions for sine, cosine, tangent, cosecant, secant, and cotangent; unit circle definitions for all trig functions; range, domain and period for each of the trig functions; inverse trig function notation as well as domain and range.

And you have trigonometry laws and identities such as: law of cosines, law of sines, and law of tangents; tangent identities, reciprocal identities, Pythagorean identities, periodic identities, even/odd identities, double angle identities, half angle identities, product to sum identities, sum to product identities, sum/difference identities, and cofunction identities; Mollweide’s formula.

Calculus

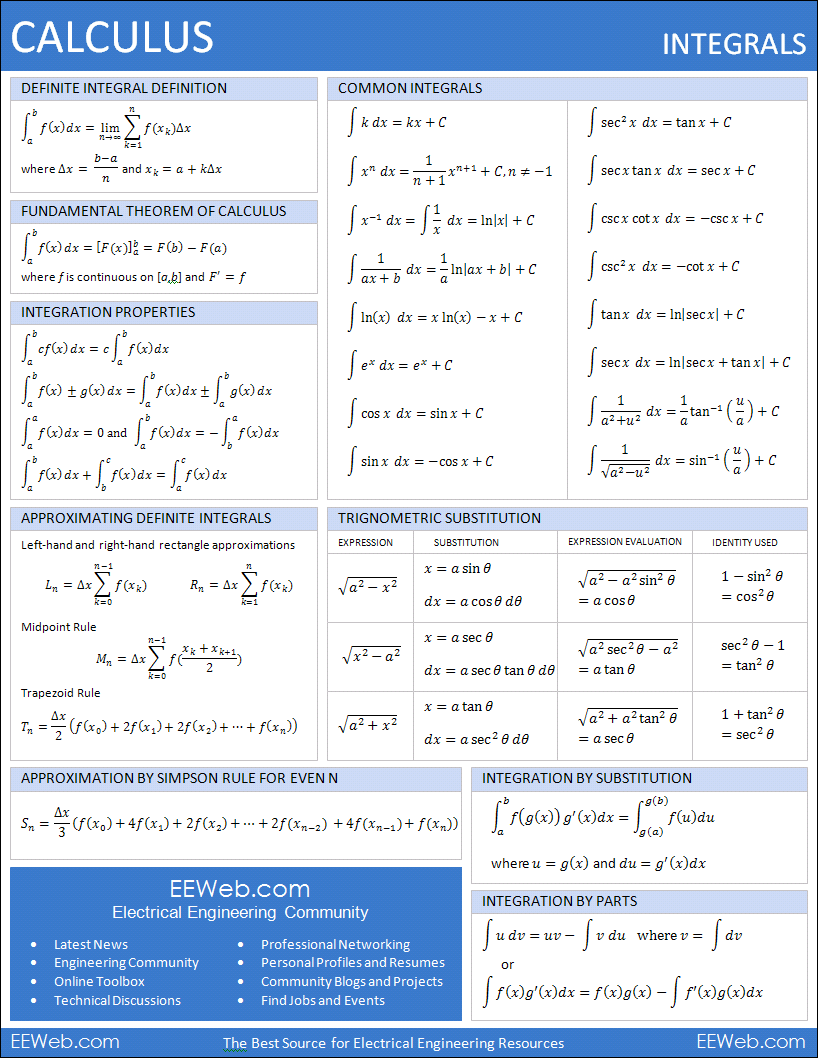
In Calculus Derivatives and Limits you have: mean value theorem, derivative’s basic properties; common derivative formulas; product rule, quotient rule, power rule, chain rule, and L’Hopital’s rule; properties of limits, limit evaluations at infinity; limit evaluation method for factoring and cancelling.

In Calculus Integrals you have: fundamental theorem of calculus, integration properties, methods for approximating definite integrals such as left hand rectangle, right hand rectangle, midpoint rule, trapezoid rule, and Simpson’s rule; common integrals; trigonometric substitution when using integrals; integration by substitution as well as the integration by parts.

Calculating Derivatives

I wanted to focus here on how to get the derivative of the composition of two or more functions as you will need this in understanding the backpropagation algorithm used in machine learning

A composition of function is defined as:

$ h(x) = f(g(x)) $

The derivative then is defined as, using the chain rule depicted in the previous infographic for the calculus derivatives and limits:

$ \frac{d}{dx}(f(g(x))) = f’(g(x)){\cdot}g’(x) = \frac{df}{dg}{\cdot}\frac{dg}{dx} $

Let’s use a simple example. Say you have this function:

$ A = 1 + B^2 $

And $ B $ is also another function:

$ B = \frac{1}{1 + C} $

And $ C $ is yet another function (we will be using a composition of three functions for this example):

$ C = 2x $, where $ x $ has a value of $ 5 $.

Get the derivative of $ A $ with respect to $ x $, in other words, what’s the effect on the output $ A $ given a change in variable $ x $?

Using substitution, you will end up with this all encompassing single function:

$ A(x) = 1 + {\frac{1}{1 + {2x}}}^2 $

You can try to get the derivative of this function straight away, but in cases where you have a more complex looking function it might be difficult. This is where the chain rule can be useful. Using the chain rule, we can have:

$ \frac{dA}{dx} = A’(B(C(x))){\cdot}B’(C(x)){\cdot}C’(x) $

$ = \frac{dA}{dB}{\cdot}\frac{dB}{dC}{\cdot}\frac{dC}{dx} $

Then we get the derivatives for $ A $, $ B $, and $ C $ separately.

For the first derivative,

$ \frac{dA}{dB} = \frac{d}{dB}(1 + B^2) $

, since derivative of a constant is 0 and using power rule you get

$ = 0 + 2B = 2B $

For the second derivative,

$ \frac{dB}{dC} = \frac{d}{dC}(\frac{1}{1 + C}) $

, using quotient rule you get

$ = \frac{0{\cdot}(1 + C) - 1{\cdot}1}{(1 + C)^2} = \frac{-1}{(1 + C)^2} $

And for the third derivative,

$ \frac{dC}{dx} = \frac{d}{dx}(2x) = 2{\cdot}C’(x) = 2 $

Multiplying them all together, we have:

$ A’(x) = 2B{\cdot}(\frac{-1}{(1 + C)^2}){\cdot}2 $

You can simplify that equation further or substitute with values to get the derivative, since we know $ x = 5 $.

So there you go. Having been able to get the derivative is a step closer to appreciating Math again, at least for me. And having a good knowledge of different Maths will definitely serve you well not just in the area of AI, but in games, financial, blockchain and metaverse.

References